A parallelogram must be a rhombus if its diagonals – A parallelogram is a quadrilateral with two pairs of parallel sides. A rhombus is a parallelogram with all four sides equal in length. In this article, we will explore the conditions under which a parallelogram must be a rhombus, and we will provide examples of parallelograms that are not rhombuses and rhombuses that are not parallelograms.
The properties of parallelograms and rhombuses make them useful for a variety of applications in architecture, engineering, and design. For example, parallelograms are used to create floor plans and roof trusses, and rhombuses are used to create decorative patterns and mosaics.
A Parallelogram Must be a Rhombus if its Diagonals

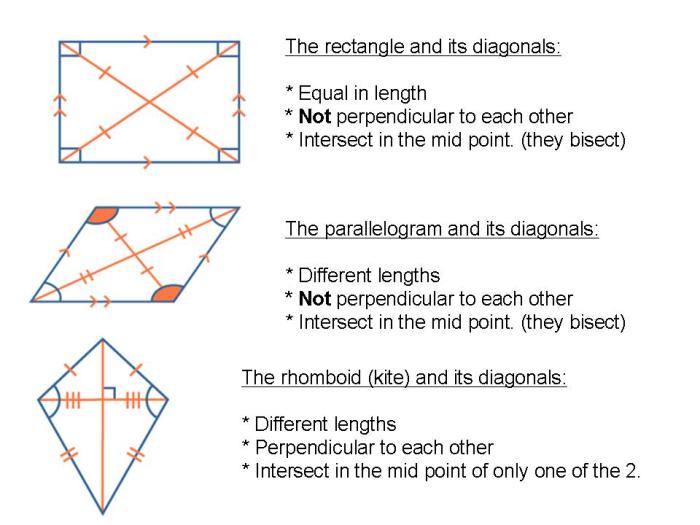
In geometry, a parallelogram is a quadrilateral with two pairs of parallel sides. A rhombus is a parallelogram with all four sides equal in length. If the diagonals of a parallelogram bisect each other, then the parallelogram must be a rhombus.
Properties of Parallelograms
- Opposite sides are parallel and equal in length.
- Opposite angles are equal.
- The diagonals bisect each other.
Properties of Rhombuses
- All four sides are equal in length.
- All four angles are equal.
- The diagonals are perpendicular to each other.
- The diagonals bisect each other.
Conditions for a Parallelogram to be a Rhombus, A parallelogram must be a rhombus if its diagonals
A parallelogram must be a rhombus if any of the following conditions are met:
- The diagonals bisect each other.
- The diagonals are perpendicular.
- The diagonals are equal in length.
Geometric Reasoning
The geometric reasoning behind these conditions is that if any of these conditions are met, then the parallelogram must have all four sides equal in length and all four angles equal. This is because the diagonals of a parallelogram bisect each other if and only if the parallelogram is a rhombus.
Examples of Parallelograms and Rhombuses
Here are some examples of parallelograms that are not rhombuses and rhombuses that are not parallelograms:
- A rectangle is a parallelogram that is not a rhombus.
- A square is a rhombus that is also a parallelogram.
Applications of Parallelograms and Rhombuses
Parallelograms and rhombuses are used in a variety of applications, including:
- Architecture
- Engineering
- Design
The properties of these shapes make them useful for a variety of purposes, such as creating strong and stable structures, designing aesthetically pleasing objects, and solving geometric problems.
Helpful Answers
What is a parallelogram?
A parallelogram is a quadrilateral with two pairs of parallel sides.
What is a rhombus?
A rhombus is a parallelogram with all four sides equal in length.
What are the conditions under which a parallelogram must be a rhombus?
A parallelogram must be a rhombus if its diagonals bisect each other.